Parallel plate capacitance approximation and limitations caused by the fringing effect1 June 2020

Introduction
This article was started a long time ago and while investigating its topic of interest I stumbled upon a different subject which quickly materialized in this interesting study. The present article initiates a small series of posts dedicated to investigating the limitations of different easy and straightforward analytical approximations. For today, I directed my attention to studying the parallel plate approximation used to calculate the capacitance between two copper planes separated by a dielectric. This approximation does not take into account the fringe fields at the edges of the copper electrodes, which in some cases can become a large source of error.
Like I mentioned in previous articles, capacitance is worth investigating since any interconnect from the signal and power integrity field can be characterized as a simple RLCG model at least as a first order model. Certain formulas exist and help to the characterization of different circuit elements but as any approximation, these also have limitations. If you do not want to go beyond the fence, you have to know where the fence is situated. In other words, it is important to understand these limitations in order to avoid possible errors.
In this article I evaluate different aspect ratios Width/Height (W/H) capacitive structures to determine the limitations of the parallel plate approximation. Cases where the dielectric extends beyond the edges of the copper planes named power puddles are also studied. In the end, once the capacitance addition caused by the fringing effect is determined, I use the corrected parallel plate formula to calculate the capacitance of a small 3D capacitive structure and I match the analytical results with simulation data.
Materials and Methods
The capacitance between two parallel plates can be calculated using Equation 1, were W, H and Len are the width, height and length of the structure as displayed in Figure 1 and ε0 is the vacuum permittivity equal to 0.225 pF/inch. εr is the electrical relative permittivity referred as Dk in this work and is equal to 1 for vacuum and 4.4 for FR4 epoxy. However, Dk varies slightly with frequency due to dipole orientation effects as discussed in a previous blog article, Frequency-Domain characterization of FR-4 dielectric using Djordjevic- Sarkar algorithm. If the capacitance per unit length is required, Equation 2 which resulted by dividing the expression from Equation 1 with the length of the structure is used. In this current investigation, unless otherwise mentioned, all the capacitance values are given per unit length (even if the subscription from Clen is omitted).
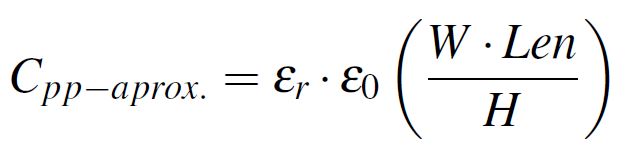 Equation 1: Parallel plate approximation
Equation 1: Parallel plate approximation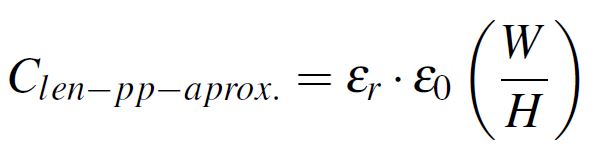 Equation 2: Parallel plate approximation per unit length
Equation 2: Parallel plate approximation per unit length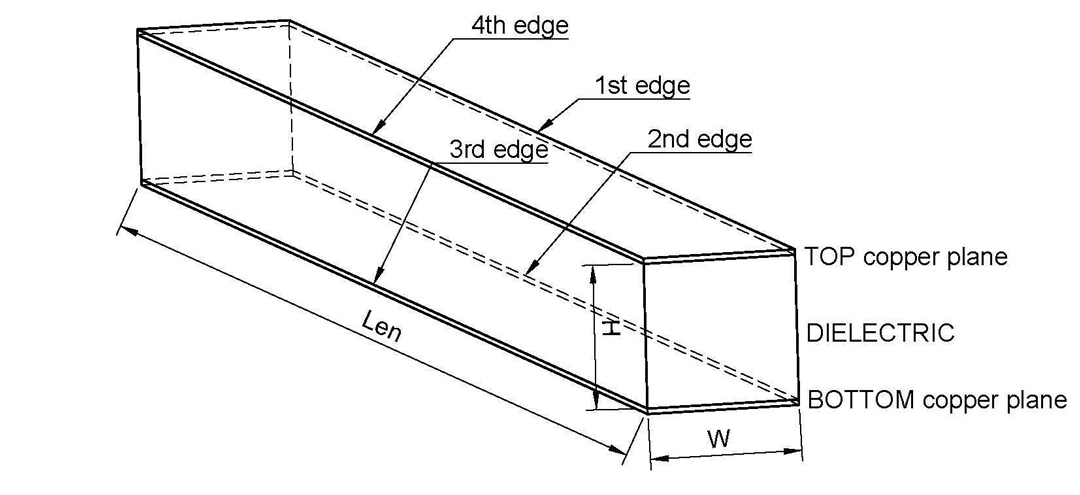 Figure 1: Structure of a parallel plate capacitor, with two copper electrodes separated by a
dielectric. Results in this investigation are given per unit length, unless otherwise mentioned.
Moreover, fringe field capacitance is given per unit length per individual edge of conductor.
Figure 1: Structure of a parallel plate capacitor, with two copper electrodes separated by a
dielectric. Results in this investigation are given per unit length, unless otherwise mentioned.
Moreover, fringe field capacitance is given per unit length per individual edge of conductor.The formulas from Equations 1 and 2 do not take into account the fringe field lines from the edges of the two copper planes. In other words, the electric field lines close between the generically named TOP and BOTTOM plates through the dielectric material but also escape the area in the proximity of the edges, closing through air, vacuum of whatever the type of the environment is. If the fringe field contribution is small with regard to the total capacitance of the planes, this addition becomes insignificant.
In this article we investigate how large a capacitive structure must be in order for the fringe field contribution to become negligible. The structures investigated are parallel plate capacitors simplified to a 2D geometry of a transversal plane sectioning the complete structure. Since only 2D structures are investigated, all the results are given per unit length. It was observed that if the structure is large enough with a high W/H, the capacitance contribution of the fringe field saturates to a constant value. This contribution called Clen-fringe is also in this work given per unit length and is furthermore expressed per edge of conductor. In other words, for the structure from Figure 1 the total corrected capacitance can be calculated using Equation 3.
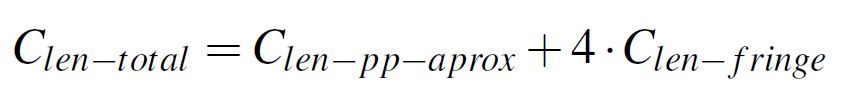 Equation 3: Total capacitance per unit length
Equation 3: Total capacitance per unit lengthThe error of using the parallel plate approximation is calculated by dividing the fringe field contribution to the total capacitance of a structure, as is numerically expressed in Equation 4. The error results are as usual presented in percents.
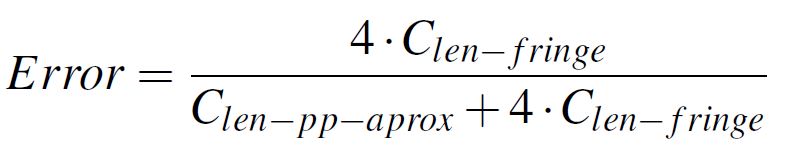 Equation 4: Error of using parallel plate approximation
Equation 4: Error of using parallel plate approximationLastly, the material through which the fringe field lines close is also of interest. In the case of parallel plate structures such as the case from Figure 1, this material is nothing more than air or vacuum (in rare and special occasions such as the case of a board immersed in water this material could differ from air). However, usually found in practical applications are not the above described structures but the ones in which the dielectric extends far beyond the edges of the copper planes. This is the case of islands from power planes located on two different layers of a circuit board, reason why this structures are also called power puddles. In this work I investigate both parallel planes and power puddles, with some interesting variations resulting in the end for both of these structures.
Simulation setup
A simulation tool as ANSYS 2D Extractor provides the capacitance of a structure while also including all the second-order effects such as fringing fields. In this way, the results from the simulation tool are considered in this investigation as total capacitance with the fringing effect also included while the parallel plate approximation includes only the capacitance of the planes. Since the geometry was simplified to a 2D plane resulted by sectioning the 3D geometry with a transversal plane, ANSYS 2D Extractor was suited for this investigation. I studied in this article both parallel plate structures (Figure 2 right side) and also power puddles (Figure 2 left side). While investigated parallel plate structures I extracted results for both the case when plates are filled with air (Dk = 1) and also with FR4 epoxy (Dk = 4.4). In the case of power puddle structures I only considered the case of a FR4 epoxy dielectric fill. Simplifying the geometry to a 2D transversal section provided an extremely reduced and high accuracy simulation.
The structures from Figure 2 were parameterized with the Height (H) and Width(W) available for various sweeps. By keeping the H to a fixed 20 MILs value and varying the W from 5 to 600 (aspect ratios from 0.25 to 30) a total of 45 simulation points were obtained for each of the three cases: parallel plates with air or FR4 dielectric and power puddle with FR4 dielectric. ANSYS 2D Extractor provided the results exactly in the way needed for this investigation, as RLCG per unit length.
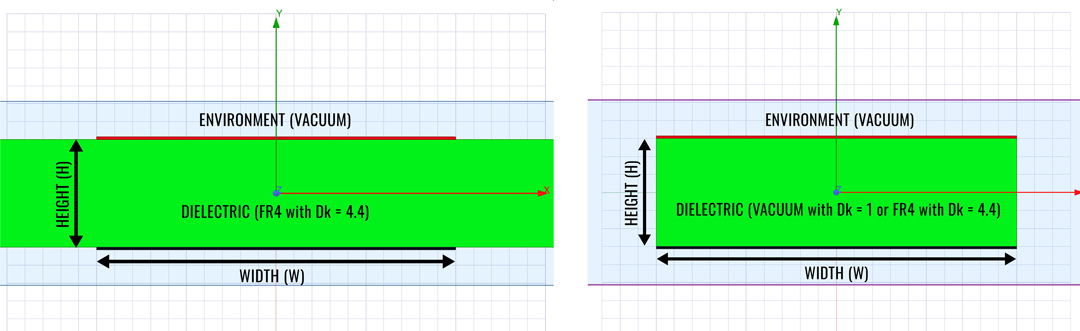 Figure 2: Parameterized geometries used in this investigation. From left to right, the one
used for power puddles and the one used for parallel plate.
Figure 2: Parameterized geometries used in this investigation. From left to right, the one
used for power puddles and the one used for parallel plate.As mentioned in the Introduction, the Dk of a dielectric material is not perfectly constant and actually varies slightly with the increase of frequency. In this investigation, causal materials are disabled, meaning that ANSYS 2D Extractor and HFSS do not implement the Djordjevic-Sarkar algorithm for the Dk of the materials involved. I opted for this setting which is in no case practical for real simulations to force the software tools to consider a precisely fixed Dk of 4.4 for the FR4 epoxy regardless of frequency. If you are interested how a frequency dependence dielectric constant should be set in ANSYS material libraries, check out this previous article where I broadly discuss this topic.
Because causal materials were disabled in this specific investigation, the frequency where the capacitance extraction was performed in ANSYS 2D Extractor is not of interest. Extracting it at 100 kHz or 100 MHz would have provided the same capacitance results. I should mention also that ANSYS 2D Extractor is only a quasi-static field solver, limitation which raised no issues in this specific study where transmission line effects were not of interest.
For high aspect ratios, the fringe capacitance was observed to stabilize at a fixed value. For both types of structures I was also interested in the error committed when using only the parallel plate formula. In this way, by using Equation 4 for high aspect ratios above the point where Clen-fringe becomes constant, I obtained the error possibly committed by not taking into account the fringe field contribution.
In the end, I also simulated a full 3D structure of 200·20·1000 MIL visible in Figure 3 in ANSYS HFSS. I obtained the total capacitance of the structure using Equation 3. The result from the corrected approximation perfectly matched the impedance profile of the structure provided by the simulator validating once again the findings of this work.
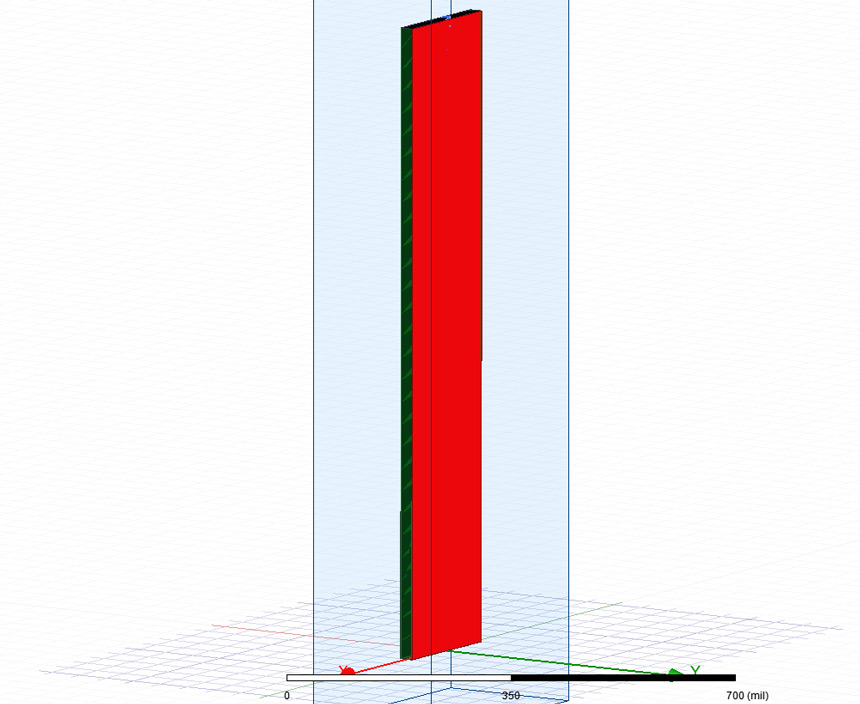 Figure 3: Small parallel plate capacitive structure with fixed 200·20·1000 MILs dimensions.
3D Design simulated in ANSYS HFSS to investigate the effect of fringe fields.
Figure 3: Small parallel plate capacitive structure with fixed 200·20·1000 MILs dimensions.
3D Design simulated in ANSYS HFSS to investigate the effect of fringe fields.Dissemination and results
I mention that there is no tabulated data included in this part of the article due to the large size of the dataset. However, all the important results are displayed in the form of graphs in this section and further discussed. I start the dissemination and results part with the parallel plate structure. This geometry was investigated in two cases: the planes filled with air (Dk = 1) and with FR4 epoxy (DK = 4.4). Height was kept to a fixed value of 20 MILs and width was varied from 5 to 600 MILs (aspect ratios from 0.25 to 30).
The Clen-fringe was extracted by subtracting from the value provided by the simulator the one from Equation 2 corresponding to the parallel plate approximation. The result was once again divided by 4 to obtain a value per edge of conductor. The variation of Clen-fringe with the aspect ratio is provided in Figure 4 for Dk = 1 and in Figure 5 for Dk = 4.4. Note that there is almost no difference between these two graphs since they both describe the fringe fields through the same environment material, the air surrounding this structure.
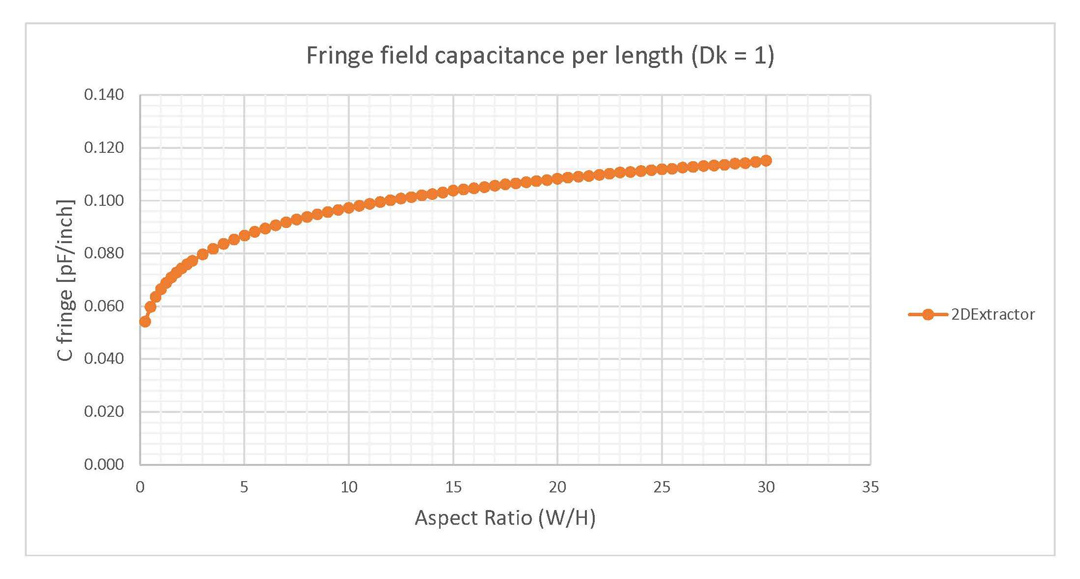 Figure 4: Fringe field capacitance of parallel plates when the dielectric is vacuum (Dk = 1).
Results are given per length per edge of conductor.
Figure 4: Fringe field capacitance of parallel plates when the dielectric is vacuum (Dk = 1).
Results are given per length per edge of conductor.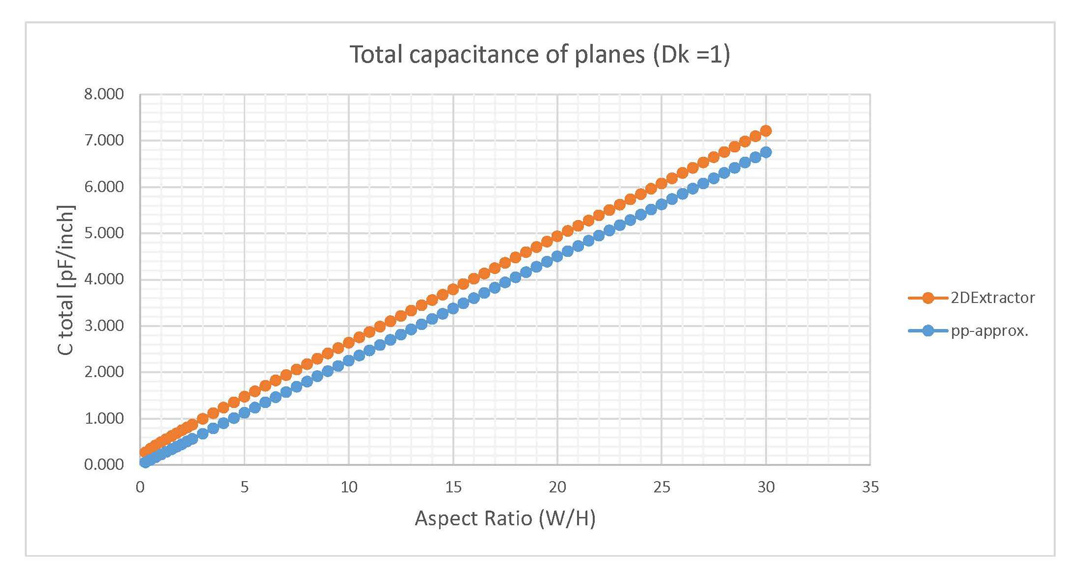 Figure 5: Fringe field capacitance of parallel plates when the dielectric is FR4 epoxy (Dk =
4.4). Results are given per length per edge of conductor.
Figure 5: Fringe field capacitance of parallel plates when the dielectric is FR4 epoxy (Dk =
4.4). Results are given per length per edge of conductor.In Figures 6 and 7 the capacitance of planes is plotted for the same parallel plate structures in the case of air dielectric fill or FR4 epoxy. These graphs include both results from 2D Extractor and also from the parallel plate approximation. In the case of plates filled with air, the difference between the parallel plate approximation and the 2D Extractor is higher than in the case of plates filled with FR4 epoxy, which generates a higher error in the first case. However, the capacitance addition caused by the fringe fields is the same for both of these cases. These previous observations are explained by the fact that in the case of FR4 epoxy the capacitance located inside the parallel plates captured by the approximation from Equation 2 is significantly higher than the fringe field addition.
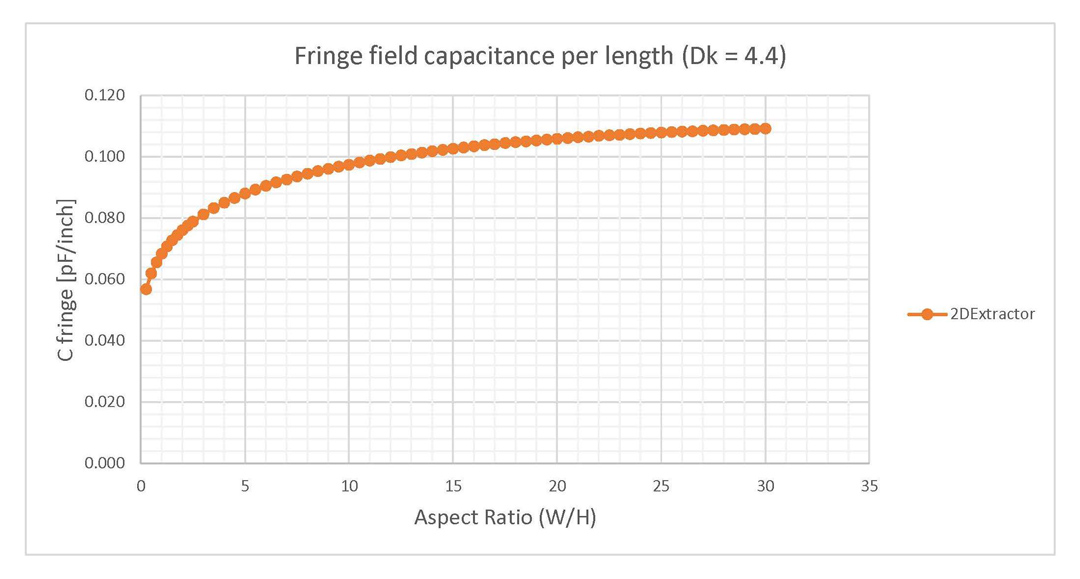 Figure 6: Total capacitance for parallel planes, comparison between the parallel plate approximation
and 2DExtractor (Dk = 1).
Figure 6: Total capacitance for parallel planes, comparison between the parallel plate approximation
and 2DExtractor (Dk = 1).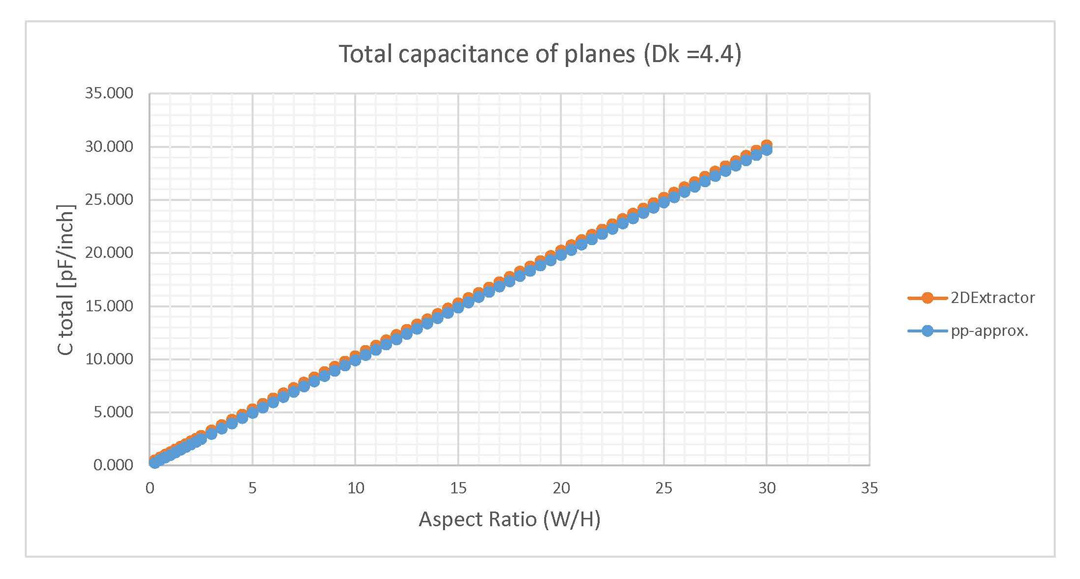 Figure 7: Total capacitance for parallel planes, comparison between the parallel plate approximation
and 2DExtractor (Dk = 4.4). Difference of values is smaller than in the case of Dk = 1.
Figure 7: Total capacitance for parallel planes, comparison between the parallel plate approximation
and 2DExtractor (Dk = 4.4). Difference of values is smaller than in the case of Dk = 1.The most important result from the investigation so far is that the fringe capacitance saturates to a fixed value around 0.11 pF/inch per edge of conductor for parallel plate structures situated in air. This result is independent of the dielectric height, the only condition being the aspect ratio to be higher than 10. This assumption is verified by performing a variation of 20 values for W and H, all with the aspect ratio held constant to 10. The results from Figure 8 validated this assumption, with the fringe capacitance constantly situated around 0.10 pF/inch per edge of conductor for any W and H value as long as their ratio was fixed to 10.
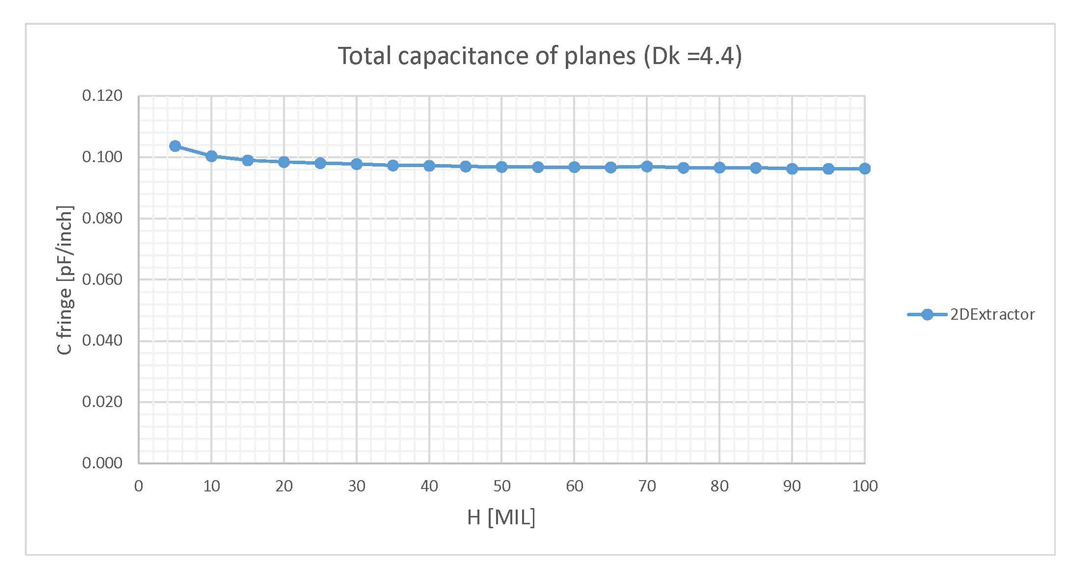 Figure 8: Total capacitance for parallel planes when height H is varied from 5 to 100 but the
aspect ratio W/H is fixed to 10. Results are given per length per edge of conductor.
Figure 8: Total capacitance for parallel planes when height H is varied from 5 to 100 but the
aspect ratio W/H is fixed to 10. Results are given per length per edge of conductor.For the parallel planes structures I also investigated the error committed by using only the approximation from Equation 2 and not taking into account the fringe field effect. Already observed in Figures 6 and 7 and briefly discussed above, this error is now plotted in Figure 9. As you can see, only aspect ratios higher than 10, the point where Clen-fringe saturates to a fixed value were used in this sweep.
Notice from Figure 9 that the error is lower for plates filled with air as compared to the ones filled with FR4 epoxy. For an aspect ratio of 10, this error is 20% in the case of air and drops to 5% for FR4 epoxy. This error graph is a good figure of interest when using the parallel plate approximation to investigate the capacitance between two parallel planes.
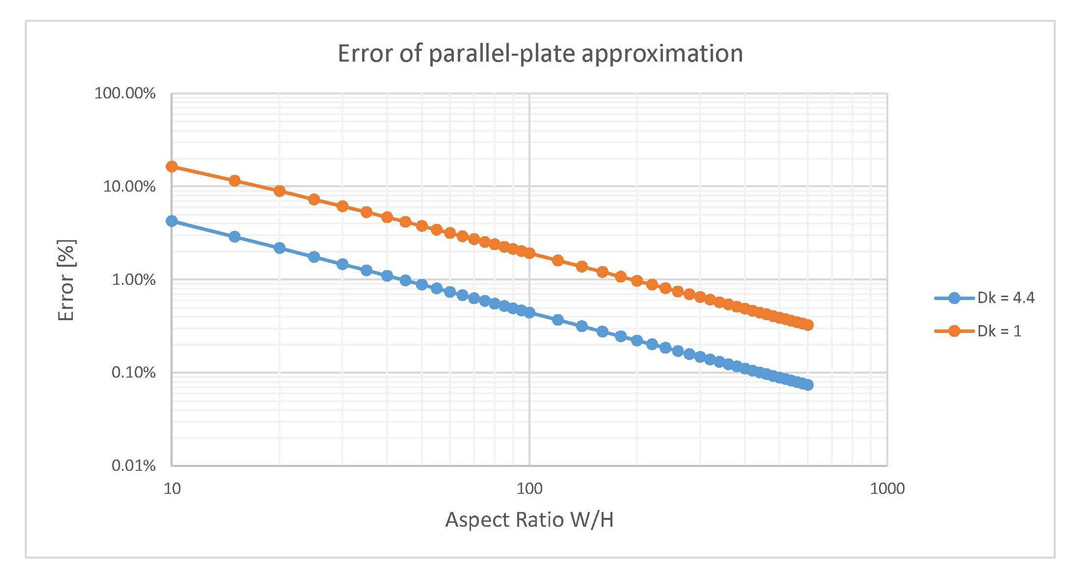 Figure 9: Error of parallel plate approximation for parallel plane structures when the dielectric
is vacuum (Dk = 1) and FR4 epoxy (Dk = 4.4).
Figure 9: Error of parallel plate approximation for parallel plane structures when the dielectric
is vacuum (Dk = 1) and FR4 epoxy (Dk = 4.4).Secondly, I also investigated the power puddle structures from the left side of Figure 2, where only a FR4 epoxy fill was of interest. I mention that this type of structures is what you would usually encounter in a circuit board and results from two partial power and ground planes, hence its name. The same height of 20 MILs and variations of width from 5 to 600 MILs (aspect ratios from 0.25 to 30) were also used and the fringe field capacitance from Figure 10 resulted through the same methods already discussed. Observe that this time the fringe field capacitance is higher, settling around the value of 0.20 pF/inch of conductor edge for aspect ratios higher than 10. This increase in the fringe capacitance was expected due to the fact that now the fringe field lines are closing through the FR4 dielectric material.
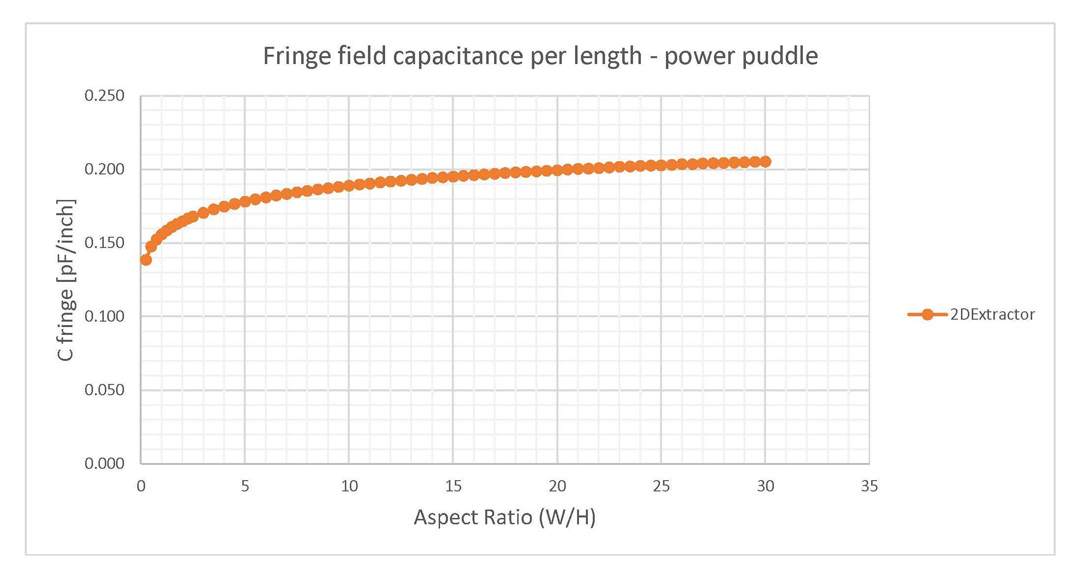 Figure 10: Fringe field capacitance of power puddles. Results are given per length per edge
of conductor.
Figure 10: Fringe field capacitance of power puddles. Results are given per length per edge
of conductor.The error of using only the parallel plate approximation for power puddles was also investigated using Equation 4 and results are displayed in Figure 11. Since the fringe field capacitance in this case is higher than in the case of parallel plane structures, the error is also higher. For the same aspect ratio of 10 is observed that now the error is around 9% while previously was only 5%.
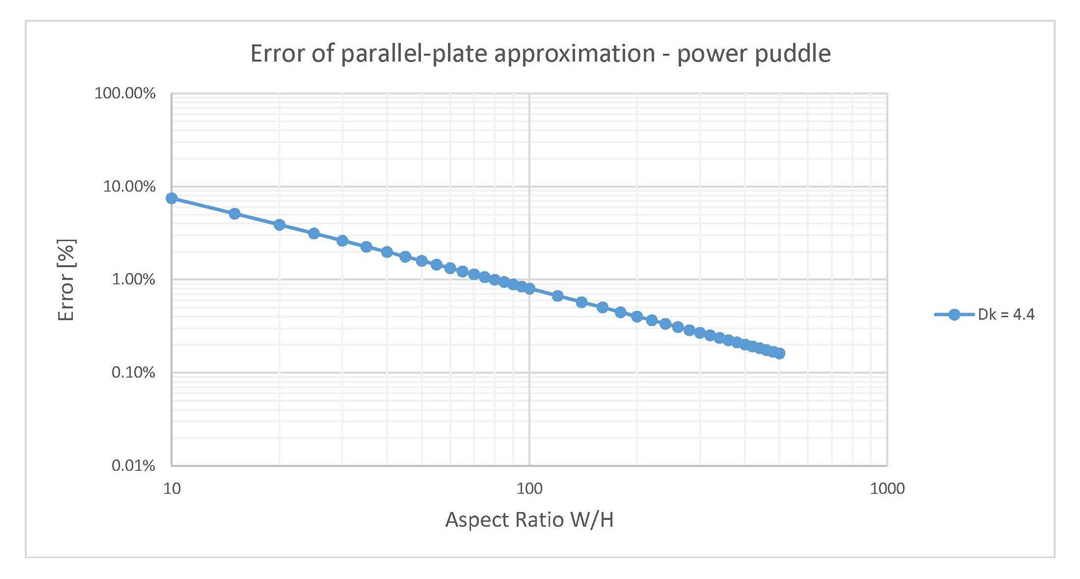 Figure 11: Error of parallel plate approximation for power puddle structures. The dielectric
is FR4 epoxy (Dk = 4.4).
Figure 11: Error of parallel plate approximation for power puddle structures. The dielectric
is FR4 epoxy (Dk = 4.4).This error graph is also a good figure of interest when using the parallel plate approximation to investigate the capacitance of power puddles. Observe that to obtain a lower than 1% error, an aspect ratio above 100 is required. It might seem a lot at first, but usually power planes have a 10 MILs separation dielectric or even lower. This value leads to a 1000 MILs width which is usually found on a regular circuit board.
With all the variations performed we obtained a fringe field addition value saturated to 0.11 pF/inch of conductor edge for parallel plate structures. I investigated one capacitive structure of this type with dimensions of 200·20·1000 MILs using ANSYS HFSS. With an aspect ratio W/H = 200/20 = 10, the structure can be considered to have a constant Clen-fringe = 0.11 pF/inch of conductor edge. Using Equation 3 and the parallel plate approximation I obtained a Clen-total = 10.34 pF/inch which results in a capacitance of 10.34 pF for an 1-inch long structure. The impedance profile extracted from Z11 displayed in Figure 12 has the impedance of a 10.34 pF capacitor imposed to the graph. Observe how this structure can be perfectly approximated with a capacitor up to 0.3 GHz, a frequency corresponding to the length of 1000 MILs being equal to λ/10. In the next frequency interval from 1.5 GHz to 3 GHz the structure becomes inductive and then has a transmission line behavior, some interesting topics for future blog posts.
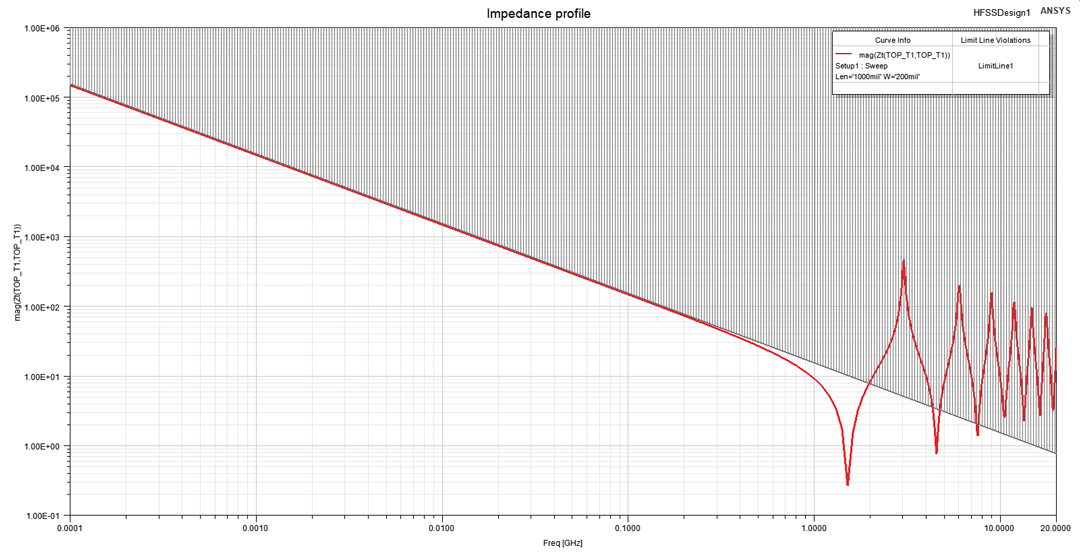 Figure 12: Impedance profile from Z11 of 3D capacitive structure from Figure 3. In can be
approximated with a 10.34 pF capacitor to the frequency of 0.3 GHz.
Figure 12: Impedance profile from Z11 of 3D capacitive structure from Figure 3. In can be
approximated with a 10.34 pF capacitor to the frequency of 0.3 GHz.Conclusion
In this article I investigated the parallel plate approximation used to calculate the capacitance between two copper planes separated by a dielectric. This approximation does not take into account the fringe fields at the edges of the copper electrodes, which in some cases can become a large source of error leading to some limitations. Dielectric materials usually have a slightly frequency dependent dielectric constant which is implemented in ANSYS products by using the Djordjevic-Sarkar algorithm, more about this discussed in a previous article here. However, in this specific investigation I ignored any frequency dependence to easily compare simulation results with the analytical approximation.
ANSYS 2D Extractor was used to extract the total capacitance between two parallel planes which of course also included the fringing effect. By subtracting from this value the result from the parallel plate approximation, the fringe field capacitance was obtained. All the results were given in a form per unit length per edge of conductor. Simulations have shown that the fringe field capacitance is 0.20 pF/inch of conductor edge in the case of dielectric fill extending beyond the edge of the copper plane or only 0.11 pF/inch of conductor edge when the dielectric fill stops at the margin of the plane. These fixed values are only valid for higher aspect ratios W/H above the threshold of 10.
Lastly, the error of using the parallel plates approximation was calculated and was found that for high aspect ratios it becomes considerably smaller. This conclusions give important insight into the limitations of using the parallel plates formula and offer a quantitative approach to correct its results if needed by adding the fringe capacitance to its result. Finally, analytical approximations are extremely useful and knowing their exact limitations is absolutely mandatory since this can make the difference between a good design and a marginal one.




